Review Pembelajaran Data Structure
Data Structure
Linked List
Linked List adalah sebuah data structure yang digunakan untuk menyimpan sebuah value dan juga untuk menyimpan sebuah element. Element pada Linked List dapat berhubungan dengan yang lain mengunakan sebuah Unary Operation(*).
Meskipun Linked List digunakan untuk menyimpan sebuah data, tetap ada perbedaan antara Linked List dengan sebuah Array. Salah satu perbedaanya adalah sifat mereka, pada Linked List bersifat statis sedangkan Array bersifat dinamis. Perbedaan lain yang dapat kita lihat terdapat pada jumlah value yang bisa disimpan pada ke 2 hal tersebut. Pada Array, kita dapat menyimpan data dalam jumlah yang telah kita tentukan tetap, sedangkan pada linked list dapat berubah-ubah sesuai dengan kebutuhan.
Pada pembelajaran linked list, terdapat juga Single Linked List yakni sebuah linked list yang hanya mempunyai 1 penghubung node terhadap node lain. Pada pembelajaran kali ini, terdapat 2 metode di dalam linked list, yaitu insertion dan delete.
Pada pembelajaran linked list, terdapat juga Single Linked List yakni sebuah linked list yang hanya mempunyai 1 penghubung node terhadap node lain. Pada pembelajaran kali ini, terdapat 2 metode di dalam linked list, yaitu insertion dan delete.
Insert Depan (Push Depan)
Metode ini digunakan pada saat kita ingin memasukan sebuah data kepada Linked List yang sudah berhubungan dan memasukan data dari depan, cara penggunaanya sebagai berikut:
void pushDepan(int y){
//buat memory dengan malloc
curr = (struct data*) malloc(sizeof(struct data));
curr->x = y;
if(head == NULL){ // Jika Linked List Kosong
head = tail = curr;
}else {
curr->next = head;
head = curr;
}
tail->next = NULL;
}
void pushDepan(int y){
//buat memory dengan malloc
curr = (struct data*) malloc(sizeof(struct data));
curr->x = y;
if(head == NULL){ // Jika Linked List Kosong
head = tail = curr;
}else {
curr->next = head;
head = curr;
}
tail->next = NULL;
}
Insert Belakang (Push Belakang)
Metode ini digunakan pada saat kita ingin memasukan data kepada Linke List yang sudah berhubungan dan memasukan data dari belakang, cara penggunaannya sebagai berikut:
void pushBelakang(int y){
//buat memory dengan malloc
curr = (struct data*) malloc(sizeof(struct data));
curr->x = y;
if(head == NULL){ // Jika Linked List Kosong
head = tail = curr;
}else {
tail->next = curr;
tail = curr;
}
tail->next = NULL;
}
void pushBelakang(int y){
//buat memory dengan malloc
curr = (struct data*) malloc(sizeof(struct data));
curr->x = y;
if(head == NULL){ // Jika Linked List Kosong
head = tail = curr;
}else {
tail->next = curr;
tail = curr;
}
tail->next = NULL;
}
Delete Depan (Pop Depan)
Metode ini digunakan pada saat kita ingin menghapus sebuah data yang sudah kita masukan sebelumnya dan menghapusnya dari depan, cara penggunaanya sebagai berikut:
void popDepan(){
if(head != NULL){
// Jika node sisa 1
if(head == tail){
free(head);
head = NULL;
} else { //node > 1
curr = head;
head = head->next;
free(curr);
}
}
}
void popDepan(){
if(head != NULL){
// Jika node sisa 1
if(head == tail){
free(head);
head = NULL;
} else { //node > 1
curr = head;
head = head->next;
free(curr);
}
}
}
Delete Belakang (Pop Belakang)
Metode ini digunakan pada saat kita ingin menghapus sebuah data yang sudah kita masukan sebelumnya dan menghapusnya dari belakang, cara penggunaanya sebagai berikut:
void popBelakang(){
if(head != NULL){
// Jika node sisa 1
if(head == tail){
free(head);
head = NULL;
} else { //node > 1
//curr diletakan di sebelah tail / sebelum tails
curr = head;
while(curr->next != tail){
curr = curr->next;
}
// Hapus node ditunjuk oleh tail
free(tail);
//kembalikan tail ke posisi node terakhir/current
tail = curr;
tail->next = NULL;
}
}
}
Hash
Hashing adalah sebuah metode dimana kita bisa menyimpan dan mengambil sebuah data atau kunci dengan cepat, biasanya kita menemukan sebuah string yang digunakan untuk metode tersebut dalam sebuah key yang pendek. Hashing juga bisa didefinisikan sebagai konsep distribusi kunci di dalam array yang kita sebut sebagai Has Table yang sudah ditentukan menggunakan fungsi bernama Hash function.
Contoh pengunaan Hash:
Sebagai contoh, kita membuah fungsi hash yang mengubah sebuah kode dalam alfabet dan mengubahnya menjadi sebuah bilangan bilat.
Misal String = ("AABBCC")
fungsi_Hash(String) = {
(banyak'a')*1 + (banyak'b')*2 + (banyak'c') *3 + ... (banyak'z') * 26 } mod 1000000
jadi jika kita masukkan string kita yang tadi
fungsi_Hash(AABBCC) = {
(2*1 + 2*2 + 3*2 + 0*4 + .. + 0*26) } mod 1000000 = 12
Di dalam pembelajaran Fungsi hash, ada beberapa sub topic bagaimana cara kita mengubah string menjadi sebuah kunci. Terdapat 5 cara yaitu:
- Mid - square = Kita menggunakan cara ini jika kunci yang akan kita gunakan adalah sebuah string dan string tersebut harus di ubah ke sebuah angka. Pertama kita kuadratkan kuncinya lalu mengekstratkkan ke tengah bits
- Division = Kita membagi sebuah string menggunakan operasi modulus, sama seperti yang sudah diterapkan sebelumnya
- Folding = Kita membagi sebuah string menjadi beberapa part lalu mengabungkannya menjadi 1 part untuk mendapatkan sebuah kunci hash
- Digit Extraction = Kita mengunakan sebuah digit yang sudah diberikan sebagai dengan sebuah alamat
- Rotation Hash = Kita mengunakan metode Division untuk mendapatkan codenya yang nantinya akan kita putar.
Collision
Pada saat kita memasukan data kedalam Hash table, tidak mungkin akan berjalan secara mulus begitu saja, pasti akan mengalami kendala tersendiri, dan kendala tersebut adalah tabrakan antar data yang ternyata pada saat kita menyimpan data tersebut memiliki key yang sama. Maka dari itu, kita harus memperbaiki masalah tersebut agar penyimpananan dapat berjalan lagi.
Terdapat 2 metode dalam Collision,
a. Linear Probing
Metode ini digunakan untuk mencari sebuah tempat yang kosong lalu menaruhkan sebuah string kedalamnya
b. Chaining
Metode ini digunakan menaruh sebuah string kedalam tempat yang terhubung pada linked list
Tree
Tree adalah sebuah non-linear data struktur yang merepresentasikan sebuah sususan yang bertingkat-tingkat diantara objek data. Untuk menentukan Tree, diperlukan beberapa consep yaitu:
a. Node yang ada diatas disebut sebagai Roor
b. Garis yang menghubungkan induk kepada anak disebut Edge
c. Node yang tidak mempunyai sebuah anak disebut dengan Leaf
d. Node yang mempunyai induk yang sama disebut Sibling
e. Degree dalam sebuah Node adalah total sub Tree dari sebuah Node
f. Depth adalah maximum degree dari Nodes di dalam Tree
g. Jika ada sebuah garis yang menghubungkan p ke q, maka p disebut dengan ancestor dari q dan q adalah sebuah descendant dari p.
Binary Search Tree
- Binary Search Tree
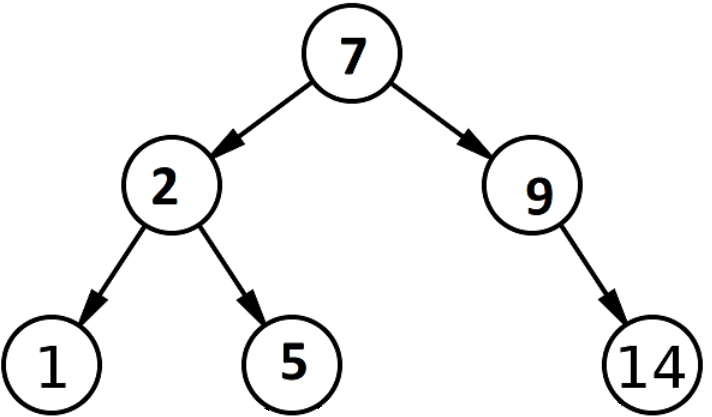
Binary Search Tree adalah sebuah bagian dari data structure yang memiliki kemampuan untuk melakukan pencarian secara cepat, melakukan sorting dengan cepat serta mudah untuk memasukan data dan menghapus data.
Di dalam Binary Search Tree dibagi menjadi 2 bagian yaitu bagian kiri dan bagian kanan, bagian kiri diisi dengan angka yang lebih kecil dari data awal, bagian kanan diisi dengan angka yang lebih besar.
- Binary Search Tree Operarions
a. Find - pencarian sebuah kunci yang ditentukan di dalam Binary Search Tree
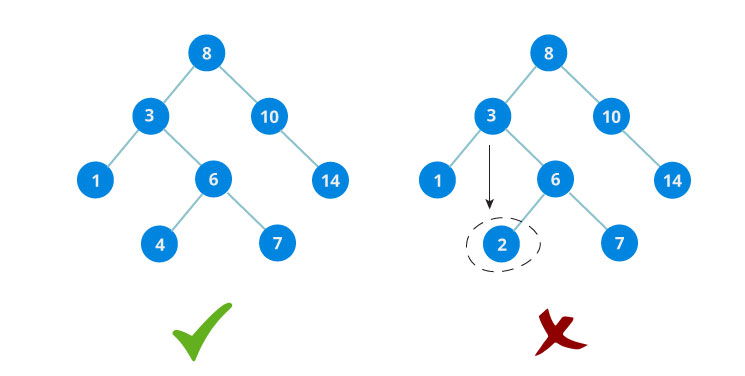
langkah yang perlu kita lakukan adalah selalu memulai dari akar pertama yaitu angka paling atas, lalu kita harus menentukan dimana letak yang sesuai untuk menaruh atau mencari sebuah angka tersebut sesuai dengan aturan yang sudah diberikan diatas tadi, jika sesuai dengan aturan, maka search berhasil.
b. Insert - Memasukan data kedalam Binary Search Tree

Langkah untuk melakukan Insert sebenarnya mirip seperti Find, namun kali ini kita menaruh angka tersebut dan akan melakuakan pengecekan ulang apakah data yang kita masukan sudah sesuai atau belum.
c. Delete - Menghapus data yang kita inginkan di dalam Binary Search Tree

Selalu memulai dengan langkah awal yaitu Find, lalu langkah selanjutnya jika sudah menemukan angka tersebut, kita akan menghapus angka yang kita cari tadi. Setelah dihapus maka kita harus melakukan pengecekan terhadap Binary Search Tree kita, apakah sudah sesuai atau belum.
void popBelakang(){
if(head != NULL){
// Jika node sisa 1
if(head == tail){
free(head);
head = NULL;
} else { //node > 1
//curr diletakan di sebelah tail / sebelum tails
curr = head;
while(curr->next != tail){
curr = curr->next;
}
// Hapus node ditunjuk oleh tail
free(tail);
//kembalikan tail ke posisi node terakhir/current
tail = curr;
tail->next = NULL;
}
}
}
Hash
Hashing adalah sebuah metode dimana kita bisa menyimpan dan mengambil sebuah data atau kunci dengan cepat, biasanya kita menemukan sebuah string yang digunakan untuk metode tersebut dalam sebuah key yang pendek. Hashing juga bisa didefinisikan sebagai konsep distribusi kunci di dalam array yang kita sebut sebagai Has Table yang sudah ditentukan menggunakan fungsi bernama Hash function.
Contoh pengunaan Hash:
Sebagai contoh, kita membuah fungsi hash yang mengubah sebuah kode dalam alfabet dan mengubahnya menjadi sebuah bilangan bilat.
Misal String = ("AABBCC")
fungsi_Hash(String) = {
(banyak'a')*1 + (banyak'b')*2 + (banyak'c') *3 + ... (banyak'z') * 26 } mod 1000000
jadi jika kita masukkan string kita yang tadi
fungsi_Hash(AABBCC) = {
(2*1 + 2*2 + 3*2 + 0*4 + .. + 0*26) } mod 1000000 = 12
Di dalam pembelajaran Fungsi hash, ada beberapa sub topic bagaimana cara kita mengubah string menjadi sebuah kunci. Terdapat 5 cara yaitu:
Misal String = ("AABBCC")
fungsi_Hash(String) = {
(banyak'a')*1 + (banyak'b')*2 + (banyak'c') *3 + ... (banyak'z') * 26 } mod 1000000
jadi jika kita masukkan string kita yang tadi
fungsi_Hash(AABBCC) = {
(2*1 + 2*2 + 3*2 + 0*4 + .. + 0*26) } mod 1000000 = 12
Di dalam pembelajaran Fungsi hash, ada beberapa sub topic bagaimana cara kita mengubah string menjadi sebuah kunci. Terdapat 5 cara yaitu:
- Mid - square = Kita menggunakan cara ini jika kunci yang akan kita gunakan adalah sebuah string dan string tersebut harus di ubah ke sebuah angka. Pertama kita kuadratkan kuncinya lalu mengekstratkkan ke tengah bits
- Division = Kita membagi sebuah string menggunakan operasi modulus, sama seperti yang sudah diterapkan sebelumnya
- Folding = Kita membagi sebuah string menjadi beberapa part lalu mengabungkannya menjadi 1 part untuk mendapatkan sebuah kunci hash
- Digit Extraction = Kita mengunakan sebuah digit yang sudah diberikan sebagai dengan sebuah alamat
- Rotation Hash = Kita mengunakan metode Division untuk mendapatkan codenya yang nantinya akan kita putar.
Collision
Pada saat kita memasukan data kedalam Hash table, tidak mungkin akan berjalan secara mulus begitu saja, pasti akan mengalami kendala tersendiri, dan kendala tersebut adalah tabrakan antar data yang ternyata pada saat kita menyimpan data tersebut memiliki key yang sama. Maka dari itu, kita harus memperbaiki masalah tersebut agar penyimpananan dapat berjalan lagi.
Terdapat 2 metode dalam Collision,
a. Linear Probing
Metode ini digunakan untuk mencari sebuah tempat yang kosong lalu menaruhkan sebuah string kedalamnya
b. Chaining
Metode ini digunakan menaruh sebuah string kedalam tempat yang terhubung pada linked list
Tree
Tree adalah sebuah non-linear data struktur yang merepresentasikan sebuah sususan yang bertingkat-tingkat diantara objek data. Untuk menentukan Tree, diperlukan beberapa consep yaitu:
a. Node yang ada diatas disebut sebagai Roor
b. Garis yang menghubungkan induk kepada anak disebut Edge
c. Node yang tidak mempunyai sebuah anak disebut dengan Leaf
d. Node yang mempunyai induk yang sama disebut Sibling
e. Degree dalam sebuah Node adalah total sub Tree dari sebuah Node
f. Depth adalah maximum degree dari Nodes di dalam Tree
g. Jika ada sebuah garis yang menghubungkan p ke q, maka p disebut dengan ancestor dari q dan q adalah sebuah descendant dari p.
Binary Search Tree
- Binary Search Tree
Binary Search Tree adalah sebuah bagian dari data structure yang memiliki kemampuan untuk melakukan pencarian secara cepat, melakukan sorting dengan cepat serta mudah untuk memasukan data dan menghapus data.
Di dalam Binary Search Tree dibagi menjadi 2 bagian yaitu bagian kiri dan bagian kanan, bagian kiri diisi dengan angka yang lebih kecil dari data awal, bagian kanan diisi dengan angka yang lebih besar.
- Binary Search Tree Operarions
a. Find - pencarian sebuah kunci yang ditentukan di dalam Binary Search Tree
langkah yang perlu kita lakukan adalah selalu memulai dari akar pertama yaitu angka paling atas, lalu kita harus menentukan dimana letak yang sesuai untuk menaruh atau mencari sebuah angka tersebut sesuai dengan aturan yang sudah diberikan diatas tadi, jika sesuai dengan aturan, maka search berhasil.
b. Insert - Memasukan data kedalam Binary Search Tree
Langkah untuk melakukan Insert sebenarnya mirip seperti Find, namun kali ini kita menaruh angka tersebut dan akan melakuakan pengecekan ulang apakah data yang kita masukan sudah sesuai atau belum.
c. Delete - Menghapus data yang kita inginkan di dalam Binary Search Tree
Selalu memulai dengan langkah awal yaitu Find, lalu langkah selanjutnya jika sudah menemukan angka tersebut, kita akan menghapus angka yang kita cari tadi. Setelah dihapus maka kita harus melakukan pengecekan terhadap Binary Search Tree kita, apakah sudah sesuai atau belum.
Comments
Post a Comment